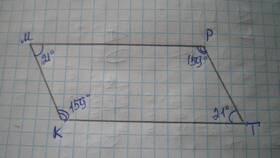
Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - не параллельны. Свойства углов трапеции имеют важное значение в геометрии.
Содержание
Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - не параллельны. Свойства углов трапеции имеют важное значение в геометрии.
Основное свойство углов трапеции
В любой трапеции сумма углов, прилежащих к боковой стороне, равна 180°. Это свойство вытекает из параллельности оснований трапеции.
Формулировка теоремы
Для произвольной трапеции ABCD с основаниями AD и BC выполняется:
- ∠A + ∠B = 180°
- ∠C + ∠D = 180°
Доказательство свойства
- Рассмотрим трапецию ABCD с AD ∥ BC
- Проведем боковую сторону AB
- Углы A и B являются односторонними при параллельных AD и BC и секущей AB
- По теореме об односторонних углах их сумма равна 180°
- Аналогично доказывается для другой пары углов
| Тип трапеции | Сумма противоположных углов |
| Произвольная трапеция | 180° для каждой пары углов при боковой стороне |
| Равнобедренная трапеция | 180° (углы при каждом основании равны) |
| Прямоугольная трапеция | 180° (один угол равен 90°) |
Пример расчета
Дана трапеция ABCD с AD ∥ BC. Известно, что ∠A = 65°. Найти ∠B.
- По свойству трапеции: ∠A + ∠B = 180°
- 65° + ∠B = 180°
- ∠B = 180° - 65° = 115°
Практическое применение
- Решение геометрических задач на нахождение углов
- Построение трапеций по заданным параметрам
- Доказательство других свойств четырехугольников
- Применение в архитектуре и инженерных расчетах
Важные следствия
- В трапецию можно вписать окружность, если сумма длин боковых сторон равна сумме длин оснований
- Около трапеции можно описать окружность только если она равнобедренная
- Высота трапеции может быть найдена через тригонометрические функции углов
Знание свойств углов трапеции является фундаментальным для решения широкого круга геометрических задач и имеет практическое применение в различных областях.
