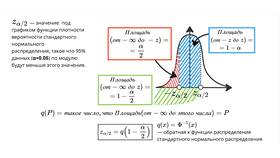
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит неизвестный параметр генеральной совокупности. Рассмотрим методы его расчета для различных типов данных.
Содержание
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит неизвестный параметр генеральной совокупности. Рассмотрим методы его расчета для различных типов данных.
Основные понятия
- Доверительная вероятность (уровень доверия) - обычно 90%, 95% или 99%
- Точечная оценка - среднее значение выборки
- Предельная ошибка - полуширина интервала
- Объем выборки - количество наблюдений
Формула доверительного интервала
| Общий вид | ДИ = Точечная оценка ± (Критическое значение × Стандартная ошибка) |
| Для среднего | x̄ ± z*(σ/√n) или x̄ ± t*(s/√n) |
| Для доли | p̂ ± z*√(p̂(1-p̂)/n) |
Пошаговый расчет для среднего значения
1. При известном σ (стандартном отклонении генеральной совокупности)
- Вычислите среднее выборки (x̄)
- Определите z-значение для выбранного уровня доверия
- Рассчитайте стандартную ошибку: σ/√n
- Вычислите предельную ошибку: z × (σ/√n)
- Определите границы интервала: x̄ ± предельная ошибка
2. При неизвестном σ (используется t-распределение)
- Вычислите среднее выборки (x̄)
- Рассчитайте стандартное отклонение выборки (s)
- Определите t-значение для (n-1) степеней свободы
- Вычислите стандартную ошибку: s/√n
- Найдите предельную ошибку: t × (s/√n)
- Определите границы интервала: x̄ ± предельная ошибка
Критические значения для разных уровней доверия
| Уровень доверия | z-значение | t-значение (n=30) |
| 90% | 1.645 | 1.699 |
| 95% | 1.960 | 2.045 |
| 99% | 2.576 | 2.756 |
Пример расчета
Для выборки из 50 элементов со средним 100 и стандартным отклонением 15, 95% ДИ: 100 ± 1.96×(15/√50) = 100 ± 4.16 → [95.84; 104.16]
Важные замечания
При малых выборках (n<30) всегда используйте t-распределение. Убедитесь, что выполнены условия применимости (нормальность распределения, случайность выборки). Для пропорций используйте z-значения при np и n(1-p) > 10.
