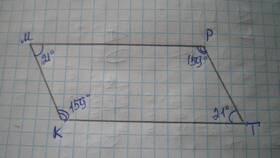
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. Эта геометрическая фигура обладает рядом интересных свойств, включая определенные закономерности в величинах своих углов.
Содержание
Основное свойство углов параллелограмма
Сумма всех внутренних углов любого параллелограмма всегда равна 360 градусам. Это свойство характерно для всех четырехугольников и вытекает из общей формулы суммы углов n-угольника: 180°×(n-2), где n - количество сторон.
Характеристики углов параллелограмма
| Свойство | Описание |
| Сумма всех углов | 360° (как у любого четырехугольника) |
| Противоположные углы | Равны между собой |
| Соседние углы | Дают в сумме 180° (являются дополнительными) |
Доказательство суммы углов
Метод разбиения на треугольники
Проведя диагональ в параллелограмме, мы получаем два треугольника. Поскольку сумма углов каждого треугольника равна 180°, то для двух треугольников получаем:
- 180° × 2 = 360°
Использование свойств параллельных линий
Учитывая, что противоположные стороны параллелограмма параллельны:
- Углы при одной стороне являются односторонними
- Их сумма равна 180°
- Таких пар углов в параллелограмме две
- 180° × 2 = 360°
Пример расчета углов
| Дано | Решение |
| Один угол равен 60° | Противоположный угол = 60° Соседние углы = 180° - 60° = 120° каждый |
| Два угла в сумме 150° | Если это соседние углы - противоречие, так как они должны давать 180° Если это противоположные углы - каждый равен 75° |
Практическое применение
Знание свойств углов параллелограмма позволяет:
- Решать геометрические задачи без дополнительных измерений
- Проверять правильность построения фигуры
- Конструировать объекты с заданными параметрами
- Вычислять неизвестные углы по известным значениям
Таким образом, параллелограмм как геометрическая фигура обладает строго определенными угловыми характеристиками, которые можно использовать при решении различных математических и прикладных задач.