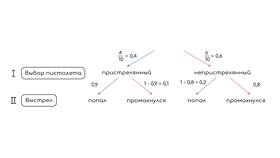
Хотя проценты часто используются для интуитивного понимания вероятности, в строгом математическом смысле вероятность имеет принципиальные отличия от процентного выражения. Рассмотрим основные причины этого различия.
Содержание
Математическая природа вероятности
- Вероятность - фундаментальное понятие теории вероятностей
- Измеряется в диапазоне от 0 до 1 (включительно)
- Нулевая вероятность означает невозможность события
- Единичная вероятность означает достоверность события
Теоретические основания
- Аксиоматическое определение Колмогорова
- Свойство нормированности (сумма вероятностей полной группы событий равна 1)
- Удобство математических операций с величинами от 0 до 1
- Согласованность с теорией меры
Практические различия
- Проценты предполагают базис 100, вероятность - базис 1
- Операции умножения вероятностей более наглядны
- Условные вероятности удобнее выражать в долях единицы
- Совместимость с логическими операциями (0 - ложь, 1 - истина)
Сравнительная таблица
| Характеристика | Вероятность | Проценты |
| Диапазон значений | [0, 1] | [0%, 100%] |
| Базис для расчетов | 1 | 100 |
| Умножение величин | P(A∩B) = P(A)×P(B) | Требуется пересчет |
Когда используют проценты
- Для приближенных бытовых оценок
- В статистических отчетах для наглядности
- При сравнительном анализе данных
- В финансовых и социологических исследованиях
Хотя перевод вероятности в проценты (умножением на 100) возможен и иногда используется, в строгих математических выкладках предпочтительна шкала от 0 до 1. Это сохраняет точность вычислений и соответствует теоретическим основам теории вероятностей.
В профессиональной среде математиков, физиков и статистиков работа с вероятностями в долях единицы считается стандартом, обеспечивающим корректность сложных расчетов и последовательность научных публикаций.